E. coli

Summary

Working with Dr. Sarah Marzen at Scripps College, I adapted a differential equation into Python to fit a model of E. coli predicting the chemical concentration of allolactose in its environment. I solved the differential equation in Python for a single input function, used the Euler approximation to solve it for a vector of functions, used regression analysis to predict all functions, and finally applied the virtual E. coli system to video prediction.

This work has been published in Biosystems.

Full Review

E. coli's preferred food source is glucose, but if glucose is absent, E. coli can consume other forms of sugar instead. To do this, it needs to produce the protein lactase by transcribing its lac operon gene. Ideally, the lac operon gene is only transcribed when glucose is absent so that extra energy isn't wasted on transcription. To optimize the production of lactase, E. coli should predict its environment rather than just respond to it.

Following the model of gene regulatory networks proposed by van Oudenaarden and others in their 2001 paper “Intrinsic noise in gene regulatory networks,” the state of the genetic system can be described at time t by the total number of mRNA molecules (j) that have been transcribed from the lac operon gene.

The mRNA transcribe at a rate of ⍺ per mRNA and degrade at a rate of β per mRNA.

The change in probability that there are j mRNA at time t (here, dp/dt) can be described with four components:

1. The probability that one timestep dt ago, there were j-1 mRNA and one was transcribed
2. The probability that dt ago, there were j+1 mRNA and one degraded
3. The probability that in dt, one more mRNA will be transcribed
4. The probability that in dt, one mRNA will degrade

This rate of mRNA transcription is described by the van Oudenaarden equation:

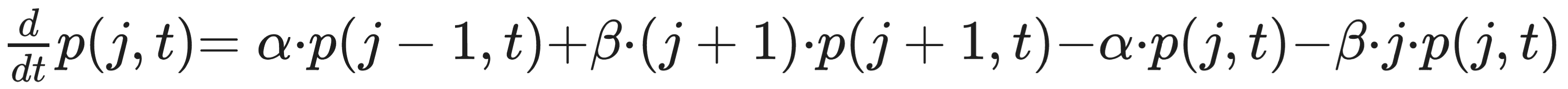
I used this model of mRNA transcription in E. coli to predict simple function inputs, as well as more complex functions such as video input. To predict the E. coli response, I used the Euler approximation to solve the van Oudenaarden differential equation for a vector of functions, and then used regression analysis to predict the functions forward.

Figure 1, created in Python, graphs the probability of having j mRNA over time. Each line represents j mRNA, with 0 ≤ j ≤ 300. At time t=0, there is a 100% probability of 0 mRNA.

Figure 2 graphs the accuracy of the video prediction as R squared over 100 time points.

This prediction ability demonstrated by groups of E. coli is an example of solving a reinforcement learning problem. The TAME framework, discussed in the associated journal paper, attempts to understand problem-solving and learning across levels of organization in living systems, and connects biological to machine learning.